Het onderwerp van dit artikel is de berekening van een luifel van polycarbonaat met uw eigen handen. We moeten leren hoe we de belangrijkste parameters van de structuur kunnen berekenen die verband houden met zijn sterkte en afmetingen. Dus laten we gaan.

Wat berekenen we
We moeten leren rekenen:
- De dikte van het polycarbonaat en de spoed van de kist afhankelijk van de verwachte sneeuwbelasting per vierkante meter.
- Afmetingen boogafdekking (wat qua geometrie neerkomt op het berekenen van de lengte van de boog).
Ter verduidelijking: we onderzoeken manieren om de boog te berekenen voor bekende straal en hoek van de sector, evenals voor het geval dat we alleen de afstanden tussen de uiterste punten van het boogoppervlak kennen.
- Minimale pijpsectie met een bekende buigbelasting.
In deze volgorde gaan we verder.
Draai- en laagdikte
Laten we beginnen met de berekening van de sneeuwbelasting.
Voordat we gaan uitzoeken hoe we een overkapping van polycarbonaat moeten berekenen, formuleren we een aantal aannames waarop de berekening is gebaseerd.
- De gegeven gegevens zijn relevant voor materiaal van hoge kwaliteit zonder tekenen van vernietiging door ultraviolette straling. Polycarbonaat zonder UV-filter wordt bros na 2-3 jaar gebruik in het licht.

- We verwaarlozen bewust de beperkte vervormingsstabiliteit van de kist, aangezien deze absoluut sterk is.
En nu - een tabel die u zal helpen bij het kiezen van de optimale dikte van polycarbonaat en de spoed van de kist.
| Belasting, kg/m2 | Afmetingen krattencel met dikte polycarbonaat, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Boog
Berekening per straal en sector
Hoe de boog voor een luifel berekenen als we de buigradius en boogsector kennen?

De formule ziet eruit als P=pi*r*n/180, waarbij:
- P is de lengte van de boog (in ons geval de lengte van een polycarbonaatplaat of een profielbuis, die een onderdeel van het frame zal worden).
- pi is het getal "pi" (in berekeningen die geen extreem hoge nauwkeurigheid vereisen, meestal gelijk aan 3,14).
- r is de straal van de boog.
- n is de booghoek in graden.
Laten we als voorbeeld met onze eigen handen de lengte van de luifelboog berekenen met een straal van 2 meter en een sector van 35 graden.
P = 3,14 * 2 * 35 / 180 = 1,22 meter.
Tijdens het werk doet zich vaak de tegenovergestelde situatie voor: het is noodzakelijk om de straal en sector van de boog aan te passen aan een vaste lengte van de boog. De redenen zijn duidelijk: de prijs van polycarbonaat is hoog genoeg om de hoeveelheid afval te minimaliseren.
Uiteraard is in dit geval het product van de sector en de straal gelijk aan P/pi*180.
Laten we proberen de boog onder een standaardplaat van 6 meter lang te passen. 6/3.14*180=343.9 (met afronding). Verder - een eenvoudige selectie van waarden met een rekenmachine in de hand: voor een boogsector van 180 graden kunt u bijvoorbeeld de straal nemen die gelijk is aan 343,9 / 180 \u003d 1,91 meter; met een straal van 2 meter is de sector gelijk aan 343,9 / 2 \u003d 171,95 graden.
Berekening door akkoorden
Hoe ziet de berekening van het ontwerp van een polycarbonaat luifel met een boog eruit als we alleen informatie hebben over de afstand tussen de randen van de boog en de hoogte ervan?
In dit geval wordt de zogenaamde Huygens-formule toegepast. Om het te gebruiken, verdelen we mentaal het akkoord dat de uiteinden van de boog verbindt, waarna we een loodlijn tekenen op het akkoord in het midden.
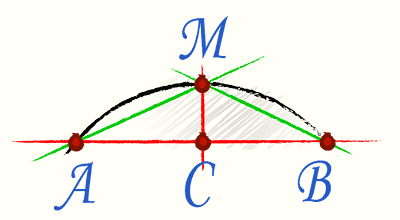
De formule zelf heeft de vorm Р=2l+1/3*(2l-L), waarbij l het AM-akkoord is en L het AB-akkoord.
Belangrijk: de berekening geeft een benaderend resultaat. De maximale fout is 0,5%; hoe kleiner de hoeksector van de boog, hoe kleiner de fout.
Laten we de lengte van de boog berekenen voor het geval dat AB \u003d 2 m en AM - 1,2 m.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 meter.
Berekening van de sectie met een bekende buigbelasting
Een behoorlijke levenssituatie: een deel van de luifel is een vizier van bekende lengte. We kunnen de pieksneeuwbelasting er grofweg op inschatten. Hoe kies je een profielpijp van zo'n sectie voor balken zodat deze niet buigt onder belasting?

Opmerking! We gaan bewust niet in op het berekenen van de belasting op de luifel. Beoordeling van sneeuw- en windbelasting is een volledig zelfvoorzienend onderwerp voor een apart artikel.
Om te berekenen hebben we twee formules nodig:
- M = FL, waarbij M het buigend moment is, F de kracht is die wordt uitgeoefend op het uiteinde van de hendel in kilogram (in ons geval het gewicht van de sneeuw op het vizier), en L is de lengte van de hendel (de lengte van de balk die de belasting van de sneeuw draagt, van rand tot puntbevestigingen) in centimeters.
- M/W=R, waarbij W het weerstandsmoment is en R de sterkte van het materiaal.
En hoe zal deze hoop onbekende waarden ons helpen?
Op zich niets. Sommige referentiegegevens ontbreken voor de berekening.
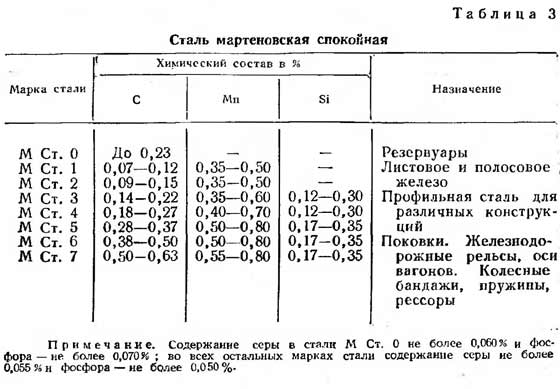
| staalkwaliteit | Sterkte (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Referentie: St3, St4 en St5 staalsoorten worden meestal gebruikt voor professionele buizen.
Nu kunnen we op basis van de gegevens waarover we beschikken het buigweerstandsmoment van de profielbuis berekenen. Laten we dat doen.
Stel dat 400 kilo sneeuw zich ophoopt op een luifel van twee meter met drie draagbalken van St3-staal.Om de berekeningen te vereenvoudigen, spreken we af dat de hele lading op de rand van het vizier valt. Uiteraard zal de belasting op elke balk 400/3=133,3 kg zijn; met een hendel van twee meter is het buigmoment gelijk aan 133,3 * 200 \u003d 26660 kgf * cm.
Nu berekenen we het weerstandsmoment W. Uit de vergelijking 26660 kgf * cm / W = 2100 kgf / cm2 (sterkte van staal) volgt dat het weerstandsmoment minimaal 26660 kgf * cm / 2100 kgf / cm2 = 12,7 moet zijn cm3.
Hoe leidt de waarde van het weerstandsmoment ons naar de afmetingen van de buis? Via de assortimentstabellen in GOST 8639-82 en GOST 8645-68 die de afmetingen van vierkante en gevormde buizen regelen. Voor elke maat geven ze het overeenkomstige weerstandsmoment aan, en voor een rechthoekige doorsnede - langs elk van de assen.
Na controle van de tabellen komen we erachter dat de minimale afmeting van een vierkante buis met de vereiste eigenschappen 50x50x7,0 mm is; rechthoekig (met verticale oriëntatie van de grotere zijde) - 70x30x5,0 mm.

Conclusie
We hopen dat we de lezer niet hebben overladen met een overvloed aan droge cijfers en formules. Zoals altijd is aanvullende informatie over de methoden voor het berekenen en ontwerpen van polycarbonaat luifels te vinden in de video in dit artikel. Succes!
Heeft het artikel je geholpen?